An element is fully integrated if the integration rule used for an
element evaluates the element matrices as accurately as analytical integration and ensures
that there are no element mechanisms associated with the element.
If the order of numerical integration used to evaluate an element matrix is lower than
the full integration rule (reduced integration), the element can exhibit what is commonly
termed a mechanism or a spurious zero energy mode. A mechanism is a mode of deformation
that causes no stress or strain to be developed as a result.
For example, the 4-noded plane continuum element is fully integrated with a 2x2
(4-point) Gaussian integration rule. If a 1-point rule (centrally located integration
point) is used to evaluate the element stiffness matrix, then the element will exhibit one
mechanism (two if the symmetrical deformation is taken into account). This mechanism
corresponds to the following element deformation
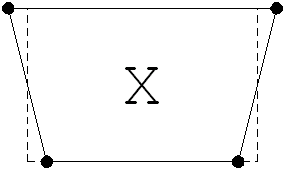
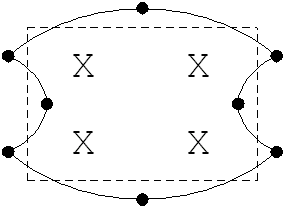
Another example is the 8-noded plane continuum element. This is fully integrated with a
3x3 (9-point) integration rule. If a 2x2 rule is used to evaluate the element stiffness
matrix, then the element will exhibit one mechanism (two if the symmetrical deformation is
taken into account). This mechanism corresponds to the following element deformation
To illustrate the effect of reduced integration on element
matrices, consider the evaluation
of the stiffness matrix of a 3-noded bar element. If
a 2-point integration rule is used a stiffness matrix is
generated that is identical to that obtained by integrating
analytically and is as follows
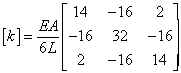
This possesses no mechanisms and is fully integrated. If
a 1-point integration rule is used, however, a mechanism
is exhibited, which can be seen by considering that the
stiffness matrix for such an element can be derived as
follows
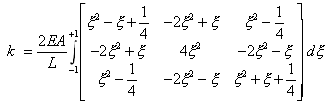
Integrating with a 1-point Gauss rule requires the integration point to be located at