Software Option for
Plus versions
Nonlinear Analysis
The LUSAS Nonlinear software option
provides the very latest powerful techniques for solving problems
having either material, geometric or boundary nonlinearity. Nonlinear
stress analysis is becoming increasingly important with designers
employing a wider variety of materials in a multitude of different
applications.
|
Compared to other finite element
systems, LUSAS contains some of the most advanced facilities for
nonlinear analysis that are available today. The Nonlinear option is
particularly effective in reducing the design and computer time
required to solve all types of complex nonlinear problems. Because
LUSAS was initially designed as a nonlinear analysis system, the
features included in the Nonlinear option can be combined with the
other LUSAS analysis options. As a result, the Nonlinear option can
not only be used to solve a multitude of problems having large
deformations, high levels of material nonlinearity and complex
boundary conditions but it can also be combined with the LUSAS Dynamic
and Thermal / Field options to solve
problems in which the effects of time and temperature are important.
The Nonlinear option includes features
such as automatic load incrementation, automatic step reduction upon
convergence failure and flexible restart facilities. These features
enable newcomers to nonlinear finite element analysis to quickly
become proficient in solving nonlinear problems.
|
 |
|
|
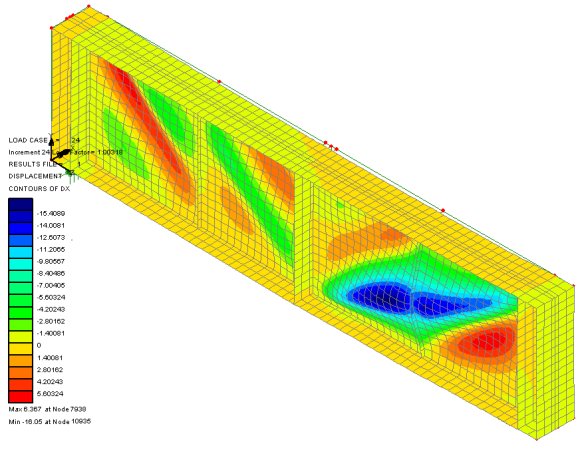
The robust automatic load
incrementation, arc length and step reduction procedures mean that, in
situations where other systems fail to converge, LUSAS reaches an
accurate solution efficiently. For maximum flexibility any chosen
incremental and iterative strategy may be specified using either load
or displacement control, based on full or modified Newton Raphson
iterations with optional line searches. Fine control is provided by
monitoring the solution using a wide selection of convergence
criteria.
The restart facility enables nonlinear
solutions which have been interrupted or terminated before completion
to be restarted without the need to re-analyse the problem from the
start. When using the restart facility analysis data can be optionally
saved at regular intervals or, for large nonlinear problems where disk
space may be a major consideration, the analysis data maybe saved for
the last converged solution(s). Analyses may be restarted from any
saved data as required.
LUSAS contains a wide selection of
material models for the analysis of elasto-plastic, ductile fracture,
cracking, damage and creep applications. There are nonlinear material
models for metals, plastics, composites, rubber, foam, soils, rock and
concrete. These material models may account for temperature dependent
effects if required. Both isotropic and anisotropic nonlinear material
models are available and material response may be dependent on the
history and direction of straining. The direction of anisotropy is
fully user definable. To ensure a fast and efficient solution the von
Mises and Hill material models use a consistent formulation in the
evaluation of the stiffness matrix which provides quadratic
convergence characteristics. The speed of stress computation has been
optimised by using the latest backward Euler technique. In addition,
material, damage and creep model interfaces are provided so user
defined material definitions may be added as required.
The creep facility allows time
dependent material behaviour to be carried out efficiently. The creep
algorithm is self-starting (it requires no preliminary linear
solution) and automatically computes the most appropriate time step
required in the transient analysis. A wide range of materials may be
modelled by combining the creep algorithm with time independent
plasticity both of which may be temperature dependent. In addition to
the standard creep laws, non-standard laws may be incorporated via a
user-defined creep interface. Note that the dynamic analysis option is
also required in addition to the nonlinear analysis option in order to
model creep.
Geometric nonlinearity needs to be
accounted for when the structure deforms to such an extent that the
original geometry and/or position and direction of the loads
significantly affect the structural behaviour. Many LUSAS elements can
accommodate large deformations and large rotations and the latest
co-rotational formulation ensures that large strains can be
accommodated when necessary.
For analyses with nonlinear boundary
conditions LUSAS has a number of features for modelling contact and
impact. Support lift-off may be modelled using a variety of nonlinear
joint models while a powerful slideline facility helps to simplify the
analysis of all types of general contact problems. The slideline and
slidesurface facility may be used to model general contact between
otherwise unconnected element groups in nonlinear and dynamic
analysis. Typical uses include problems involving friction,
impact/energy absorption and metal forming processes. A tied slideline
option also exists which can be used in linear and nonlinear analysis
to eliminate the need for a transition mesh region between areas of
the model having coarse and fine mesh densities. For sensitive contact
problems in which rapid convergence is difficult to achieve due to
large changes in forces in the contact region a close contact
detection facility is provided. This facility checks for any nodes
that are about to come into contact and creates a transition zone,
cushioning the nodes before full contact is reached. For nonlinear
static analyses where the surfaces of a slideline need to be brought
into contact under the action of the applied loading and interface
forces before the analysis proceeds a pre-contact facility is
provided. This allows the surfaces of a slideline to be defined with a
gap between them. The pre contact facility acts like a magnet in
bringing the bodies into contact to avoid unrestrained rigid body
motion. Boundary conditions can include springs and single or
multi-point constraints.
Loading may be applied as prescribed
displacements, point, distributed or body loading. This loading may be
varied over the structure using a comprehensive variation facility
and/or varied as the analysis progresses using an integral load curve
facility. Both conservative loading (where the load direction does not
change with deformation) and non-conservative loading (where the load
direction changes with deformation) can be applied. Initial or
residual stresses and strains and temperature loading can also be
specified.
In rotating machinery the effects of
rotation can have a significant effect on the natural frequencies of
the structure. Within LUSAS the load correction terms required to
accurately take account of the effects of rotation are introduced by
carrying out an initial nonlinear analysis prior to carrying out a
natural frequency analysis. For structures, such as cables in which
applied loading, initial residual stress, or varying material
properties can significantly affect the structural stiffness a
frequency analysis can also be undertaken after a nonlinear analysis.
In many application areas parts of the
structure need to be added to or removed from the finite element model
as the analysis progresses. Within LUSAS such an event can be
accommodated using the activation and deactivation facility. Any residual forces
present after activation or deactivation of elements can be
re-distributed to surrounding elements under user control. Additional
options allow the definition of relaxation at any boundary together
with the number of increments over which the activation/deactivation
takes place. This facility enables problems such as
general excavation, tunnelling and staged construction of bridges and
other structures to be
accurately modelled.
Nonlinear
Buckling
For a detailed structural
buckling assessment a geometrically nonlinear analyses should be carried
out. With this, material and boundary nonlinearity can also be
investigated if found to be required. With a geometrically nonlinear
analysis the stiffness matrix of the structure is automatically updated
between loading increments to incorporate deformations which affect the
structural behaviour (sometimes described by engineers as P-delta
effects). Nonlinear buckling can be performed on the original
structure without imperfection, or by automatically adding an
imperfection based upon a scaled deformed shape which could be from a
linear buckling model.
|
|
|
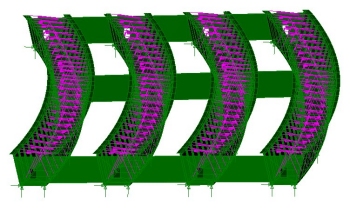
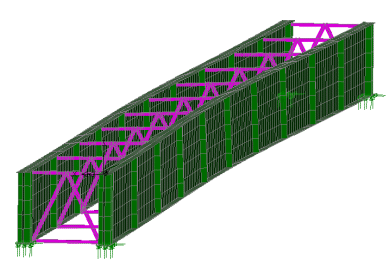
| A nonlinear buckling analysis with
LUSAS can investigate the stability of girders under self-weight
loading, imposed construction loads such as slab pours, and wind
loads. From the results obtained, members can be re-sized
accordingly and, if necessary, temporary bracing and supports can
be inserted into the model and tested to reduce the structural
response.
 See
Additional
Information - Linear - Nonlinear Buckling for more
information. See
Additional
Information - Linear - Nonlinear Buckling for more
information.
|
|
In addition to all the usual powerful
contouring, graphing and plotting features in LUSAS Graphics, a large
number of specific nonlinear results processing features are
available. These include:
- Automatic load-displacement graphs
- Viewing of material yield
- Viewing of concrete crack directions
- Graphing of analysis control
criteria
- Animation of structure deformation
- Visualisation of contact zones and
contact pressure
Find out more
|