User Area > Advice
Nonlinear load incrementation
Load incrementation controls how much load is applied in each load
increment. Load incrementation for nonlinear problems may be applied in one increment only
or gradually over a number of increments and may be specified in four ways:
Manual Load Incrementation:
The load level, comprising all load datasets assigned to a load case, is
applied in just one load increment – within which a number of iterations occur to
achieve equilibrium. A manual load increment can be invoked from the load case properties
(Nonlinear & Transient> Set…> Nonlinear> Incrementation = Manual).
As an example, consider four loadcases that are to be applied to a
structure using manual incrementation. Loadcases 1 to 4 represent applied loads of 20, 40,
60 and 80kN respectively. The first load case must be given manual nonlinear properties
– which are then automatically assumed for all subsequent load cases. The loadcase
treeview would then be as follows:
Model data
1:loadcase 1 (with specified manual NONLINEAR control)
2:loadcase 2 (with no control specified)
3:loadcase 3 (with no control specified)
4:loadcase 4 (with no control specified)
For load cases in which force loads are specified, the total values at
each step must be input. In contrast, incremental prescribed displacement loading is
additive, and hence the incremental change should be specified. The use of total
prescribed displacement loading is recommended for load curve analyses.
This form of load incrementation is the most simple to define but,
depending on the degree of nonlinearity experienced by the structure within each load
increment, convergence may not be possible. To obtain convergence in this case, it is
necessary to apply the load gradually over a number of increments. This may be performed
using manual incrementation by increasing the number of load cases and adjusting the load
levels applied in each or automatic load incrementation which performs the same task
automatically.
Automatic Incrementation:
The load level, comprising all load datasets assigned to a load case, is
applied gradually, being multiplied by a load factor that may provide either fixed or
variable loading increments. In this way each loadcase is applied over a number of load
increments – iterative procedures occurring within each increment to achieve
equilibrium. An automatic load increment can be invoked from the load case properties
(Nonlinear & Transient> Set…> Nonlinear> Incrementation = Automatic).
Automatic incrementation does not need the repetition of load cases to
achieve a load history, as required for the manual incrementation method.
As an example, consider a single loadcase representing 80kN, that is to
be applied to a structure using automatic incrementation. The loadcase is given automatic
nonlinear properties which will initially apply 10% of the load (say), gradually
increasing until 100% is achieved. The general form in the loadcase treeview will be as
follows:
Model data
1:loadcase 1 (with specified automatic NONLINEAR control)
The number of load increments produced will depend on whether uniform or
variable incrementation is selected, any imposed limits on the load factor and the degree
of nonlinearity experienced.
This form of load incrementation is more involved than manual but
responds automatically to the solution behaviour – giving the best possible chance of
convergence by the use of step reduction and arc length procedures.
Automatic incrementation is not applicable for use with a direct
integration dynamic, viscous or transient analysis.
Two methods of automatic incrementation are available:
- Uniform Incrementation: The load level
represented by the current loadcase is multiplied by
a load factor that remains constant throughout the analysis.
The value of this uniform increment is specified by
the starting
load factor. By default, uniform incrementation
is applied.
- Variable Incrementation: The load level represented by the current
loadcase is multiplied by a load factor that automatically varies according to the
iterative performance of the solution.
The load factor variation depends on the relationship between the actual
number of iterations taken for the previous increment to converge and a specified
"desired number of iterations per increment". When the actual number of
iterations taken to converge is less than the specified desired value, the load factor
will be increased and, conversely, if the number of iterations is greater than the desired
value, it will be decreased. Variable incrementation may be used in conjunction with
either constant load level or arc-length (variable load level) solution methods and is an
effective way of automatically adapting the performance of the solution procedure to the
degree of nonlinearity encountered. The overall effect is to increase and decrease the
numerical effort in the areas of most and least nonlinearity respectively.
Mixed Incrementation:
Manual and automatic load incrementation may be combined freely. When
doing so, the following conventions apply:
- Load cases may be re-specified as often as required
- If the automatic procedure is specified,
it will continue until one of the termination
criteria is satisfied
- In switching from manual to automatic
control, any loading input under the manual control
is remembered and held constant while the automatic
procedure is operating. See nonlinear
loading procedures
- In switching from automatic back to
manual control, any loading accumulated under automatic
control is forgotten and only the manual load is applied.
To include the final load level from automatic load
increments, the load datasets from which it comprises
must also be assigned to this manual load case. See
nonlinear
loading procedures
- If incremental prescribed displacements
are being used then, in any switching from one type
of control to another, the effect of prescribed displacements
will be remembered and will not need to be input again.
This is not the case for total prescribed displacements
which are total loads and operate in the same manner
as force loads. See nonlinear
loading procedures
Load Curves:
In which the variation of one or more loadcases is specified as a load
factor vs. load increment or time step load curve. They are used to simplify the input of
load data in situations where the variation of load is known and beyond the natural
capability of the manual or automatic incrementation methods. An example of this would be
the dynamic response of a pipe to a fluctuation in pressure over a given period. The data
input would consist of the definition of the load and its variation with time
The choice of incrementation method will depend on the problem to be
solved.
The original form of the Newton-Raphson procedure assumes that a
displacement solution may be found for a given load increment and that, within each load
increment, the load level remains constant. Where limit points in a structural response
are encountered (for example in the geometrically nonlinear case of snap-through failure),
constant load level methods will, at best, fail to identify the load shedding portion of
the curve and, at worst, fail to converge at all past the limit point. The solution of
limit point problems therefore leads to the development of alternative methods, including
displacement incrementation and constrained solution methods.
Constrained methods differ from constant level methods in that the load
level is not required to be constant within an increment, rather it is constrained to
follow a pre-defined path. In LUSAS, two forms of arc-length method are available:
- Crisfield’s modified arc-length procedure, in which the solution is
constrained to lie on a spherical surface defined in displacement space. For the one
degree of freedom case this becomes a circular arc.
- Rheinboldt’s arc-length algorithm, which constrains the largest
displacement increment (as defined by the predictor) to remain constant for that
particular increment.
Control of arc-length solution procedures
is via the Incrementation
section of the nonlinear control dialog. If required, the
solution may be started under constant load control and
automatically switched to arc-length control based on a
specified value of the current
stiffness parameter.
Where limit points are encountered with
arc-length invoked, LUSAS will automatically determine the
direction of loading for the next load increment from the
sign of the determinant of the stiffness matrix. This is
a reliable method in most cases; however, it will often
fail in the vicinity of bifurcation points when negative
eigenvalues may cause premature unloading. In such cases
the solution path may be optionally made dependent on the
sign of the current
stiffness parameter. This latter method is better at
coping with bifurcation points, but will always fail when
a snap-back situation is encountered. In certain circumstances,
notably in the presence of strain-softening, the arc-length
method may converge on alternative, unstable equilibrium
paths.
If an increment fails to converge within
the specified maximum number of iterations, the load level
of that increment will be automatically reduced and re-applied
when automatic load incrementation has been invoked (see
diagram below). This will be repeated according to values
specified in the step
reduction section until the maximum number of reductions
has been tried.
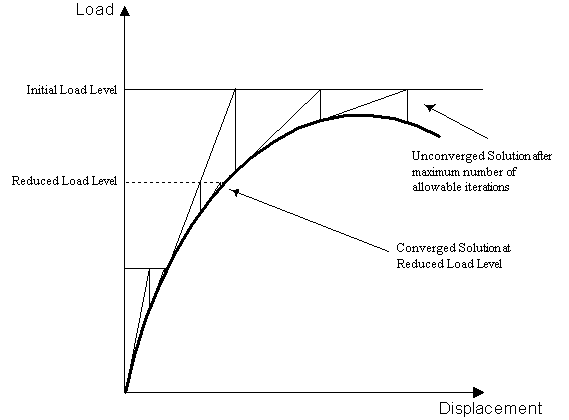
If the specified number of step reductions do not lead to convergence, a
final attempt is made to achieve a solution by increasing the original increment using a
load increase factor. This procedure has the potential to step over a difficult point in
an analysis (e.g. a bifurcation point) so that the solution can continue. If, after this,
the solution has still failed to converge the solution is terminated.
A solution using automatic load incrementation will progress until one
of the following terminating criteria is satisfied:
Where more than one criterion is specified, termination will occur on
the first.
It is usual to use the load factor to control the termination. It can
also be helpful to specify a value for the maximum number of applied increments. This
prevents an excessive number of increments being performed when variable load
incrementation is invoked, since it is possible for the load increment to so reduce that
further progress is inordinately slow – normally indicating a modelling or solution
control problem.
Failure to converge within the specified
number
of iterations will cause the failed increment to start
again, but with a reduced applied load. If required, the
solution may be forced to continue to the next load increment
if the option to "continue
solution after convergence fails" is invoked.
In addition, the solution will be terminated
if, at the beginning of an increment, more than one negative
pivot is encountered during the elimination phase of the
frontal solution method. By specifying that the solution
continues if
more than one negative pivot occurs, overrides the load
step reduction and forces the solution to continue to the
next load increment.
When using manual incrementation, these
criteria do not apply and the solution will continue until
the specified maximum number
of iterations permitted in an increment occurs or the
solution converges. For the former, the solution will not
have converged and the solution will be terminated because
step reduction is not applicable to this form of load incrementation.
For the latter, the next load increment (if present) will
commence.
The convergence criteria specify at which stage the iterative procedure
can be assumed to have restored the structure to equilibrium. The specification of
convergence involves two considerations:
- Convergence tolerance
- Convergence criteria
The convergence tolerances for the criteria
are specified in the default and advanced dialog forms of
the solution
strategy in the nonlinear control properties. The selection
of appropriate convergence criteria and their associated
tolerance values is problem dependent.
To obtain "complete" convergence, the tolerance limits would
need to be set at zero. This would be numerically too exacting and instead, small values
based on experience and general observation are used. For this reason the default settings
are recommended. If their modification is necessary, the convergence criteria must not be
too slack so as to yield an inaccurate solution nor too tight so as to waste computer time
performing unnecessary iterations.
Sensitive geometrically nonlinear problems require tight convergence
criteria whereas, with predominantly materially nonlinear problems, larger local residuals
may be tolerated.
The solution has converged if the values of all the specified criteria
at the end of an iteration are less than the tolerances specified. If a convergence
tolerance is input as zero or large, it is ignored.
The types of convergence criteria incorporated in LUSAS are as follows:
The frequency of output to the results files created by Solver can be
controlled in the output section of the nonlinear control dialog by specifying the number
of load increments to pass between writing to each file. Each result file can be
controlled separately.
The following results files are created:
- Output file: This contains an echo of all the data input as well as a
summary of the model properties. The element and node output facility (File> LUSAS
Datafile> Output…) can be used to control the type of output written to this file
and may be specified at nodal, element or Gauss point locations. Because all result data
is written to the results and restart files, the output file results are not normally
required.
- Plot file: This is the results file read by MODELLER subsequent to a
solution.
- Restart file: The restart facility enables failed or terminated analyses
to be restarted from the last saved restart results file. This is particularly useful
where the termination of the analysis was due to a failure of the solution process rather
than that of the structure. In this way, the solution may be restarted from the last
converged increment with a different or modified solution strategy. For example, a failed
increment may be restarted under either constant load or arc-length control.
- Log
file: During the course of a nonlinear analysis, information
is output to the screen or a log file, so that the performance
of the solution may be assessed.
- History file: The output of results to the selective results history
file.
|